- A linear equation in 2 variables is a straight line on a graph.
- A system of 2 Linear equations in 2 variables –
A1x + B1y = C1
A2x + B2y = C2
The 2 lines will be parallel to each other if (A1 * B2) – (B1 * A2) = 0 - If (A1 * B2) – (B1 * A2) is not 0 then, they must intersect each other.
The same problem statement could be formed into a “Linear equation” or “Quadratic function” we need to use our imagination to do so, by using the right variables.
Ex – A certain amount is equally distributed among a certain number of students. Each would get 2$ less if 10 students were more.
The above problem could be formulated in 2 equations –
Consider D = total amount to be distributed, S = Total number of students, and A=Amount per student.
- Quadratic -> (D/S) – 2 = D/(S + 10) -> 2S2= 10D – 20S
- Linear -> (A – 2) = (A * S) / (S+10) -> S = 5A – 10
The complete example is –
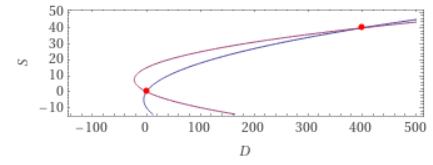
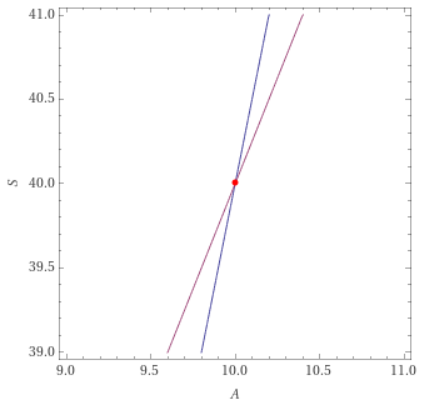
A certain amount is equally distributed among a certain number of students. Each would get 2$ less if 10 students were more and each would get 6$ more if 15 students were less. Find the number of students and the amount distributed.
If we try to solve the above example by forming a “Quadratic” or “Linear equation”, the solution is the same – D=400, S=40, and A=10
If we replace D/S by A in a quadratic, then it is getting simplified to a linear equation as well.
By this process, we are changing the curved graph of the quadratic equation to the straight line of the linear equation.